An informative guide on the linear search in Python
There are many languages, but few are as strong or as widely used as Python. A single command just only a few lines of code, making this a very accessible language. Searching finds if an element is in a list. In general, there are two kinds of searches:
- Linear Search
- Binary Search
Both methods are often used when looking for a specific item in a list.
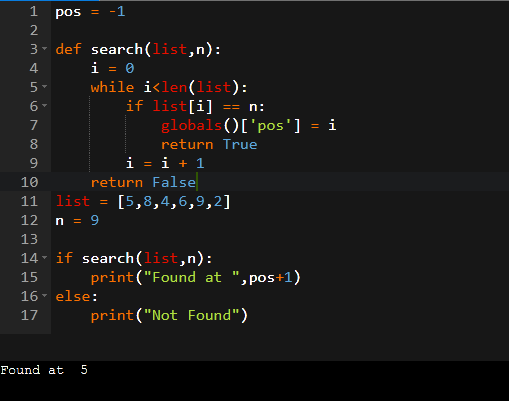
User input used in a linear search using Python
You can use linear search in Python to locate items in a list. The process is also known as a sequential search. It is the simplest search algorithm since it searches the requested element sequentially. Every factor is weighed against the target value. The element is located, and the key’s index position is returned if both criteria are met.
Principles of Linear Search
Here are the directions for finding the item in the provided list where the key is 7.
1 3 5 4 7 9
First, examine each item in list x, beginning with item 1, using the criteria “key = 7.”
Second, the key’s index position is returned if the element is located.
Third, return “element is not present” if “element” was not found.
Algorithm for Linear Search
There is a searchable key value and a list of n items. The linear search in python algorithm is shown in the following.
LinearSearch(list, key)
for each item in the list
if item == value
return its index position
return -1
Python for loop-based linear search
Linear or sequential searches include searching a list item by item to locate a match. Compared with other strategies, it is the poorest searching algorithm with worst-case time complexity O (n).
Algorithm for loop-based linear search
The user enters a searchable number, which is saved in variable n.
Array a is initialized.
Using for loop, perform the linear search.
Check if n==a[i], if true print “Number found”.
Also, return its index or position.
Iterate till you find the desired number which the user asks for.
Exit.
Linear search in python: Benefits of a Python-Based Linear-Search Application
- The linear search in Python is best employed when a key component matches the array’s first element since its execution time is 0 (n), where n is the array’s size.
- There is no change as a result of deletions or insertions. The linear search does not need categorization. Therefore, more members may be added and deleted. Similar to other search forms, algorithms may need to rearrange the list once changes have been made. Sometimes it suggests a linear search is better.
- Since a binary search needs the data to be in sorted order, a python program for linear search has the edge over it.
Frequently Asked Questions about Linear search in python
What are Python’s linear and binary search algorithms like?
Notable distinctions between linear search and binary search include:
In Linear Search:
Typically, a linear search has an O(n) time complexity (n).
As its name implies, it works best with unorganized information.
Applying a method of iteration.
The key would be located at the beginning of the list in an ideal scenario.
In Binary Search:
O(log(n)) is the typical time complexity of a binary search.
Specifically, it works well with ordered information.
Using a “divide and conquer” strategy.
In the best situation, you’ll find the answer somewhere in the center of the list.
Explanation of what is meant by “linear search”?
An element is checked off the list one by one in a linear search, which is also called a sequential search. If you want to find anything in a list or array, you can calculate a simple length and skip over any items that don’t fit the criteria. Let’s look at a basic illustration.
Let’s pretend you have a 10-element array like the one shown below:
A B C D E F G H I J
0 1 2 3 4 5 6 7 8 9
The figure that is included with this post displays a character-type array that has 10 separate values. In the scenario that the element cannot be discovered, the search for it will begin with the initial element and continue through each of the elements in turn until it is concluded that E cannot be located.